Tudo estava muito bom para os físicos e matemáticos, descrevendo o mundo em sua volta de uma forma logica usando a matemática. Até o dia em que o matemático, e cientista da computação britânico, Alan Turing, que estava tentando descrever como células de um embrião se agrupavam, em determinados
tecidos que por sua vez formariam determinados órgãos.Já parou para pensar nisso? Como essas células parecem ter esse "auto-conhecimento" de como se organizar e onde.
Turing criou equações determinando esses padrões que as células se juntavam. As células seguiam as características genéticas contidas no zigoto.
Turing realizou o primeiro passo para entender a teoria do caos, suas equações podem descrever a genética das populações e até mesmo as listras em uma zebra. Mas como assim?
Bem, para entender melhor como isso acontece podemos observar um experimento feito por Belousov Zhabotinsky.
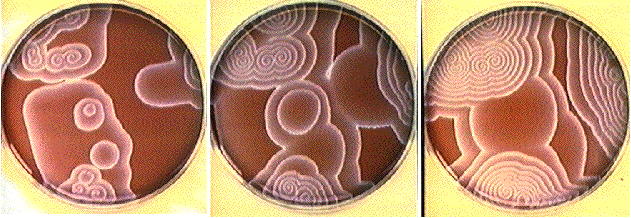
Essa reação ocorre apos misturar os seguintes elementos: Malônico acido, Bromato de Sódio, Acido Sulfúrico e ferroína.(com uma certa concentração de cada elemento.)
Apos misturar os elementos, podemos perceber algumas ondulações e cores que variam do vermelho para o azul e decaem para outras cores conforme oxidam.
A parte interessante é que cada ondulação é importantíssima para descrever a dinâmica do sistema inteiro, porem não podemos prever como essas ondas iram se comportar pois são aleatórias.
Esse mesmo comportamento pode ser observado em seres unicelulares e pluricelulares.

A imagem acima mostra amebas se organizando para formar um corpo de frutificação que gerará esporos, essa organização das amebas não é muito diferente da organização de células embrionarias em animais pluricelulares como nós.
Então isso quer dizer que também frutos dessa ondulação entre as células?
Sim, e aqui está mais um esquema. A imagem abaixo mostra uma ameba (Dictyostelium discoideum)
O esquema está mostrando desde a liberação do esporo até a formação da ameba.
Como podemos observar apos o corpo de frutificação ele libera esporos e esses esporos se desenvolvem e podemos ver o mesmo padrão de ondulações do experimento de Belousov Zhabotinsky.
A formação desse corpo de frutificação é realizado da mesma maneira, varias amebas se unem para formar este corpo. É algo incrível de se ver como elas se unem. (http://www.youtube.com/watch?v=vjRPla0BONA)
Legal, esses experimentos realmente mostram muitas peculiaridades mas o que isso tem haver com a teoria do caos?
Essa questão pode ser respondida mostrando o trabalho de um matemático chamado BenoÎt Mandelbrot.
Mandelbrot observava vários padrões criados pela natureza, padrões como cursos de rios, montanhas, etc...

Assim como os galhos de uma arvore que sempre formam forquilhas que se repetem até as menores formas.Mandelbrot criou uma equação descrevendo esse comportamento.
z=z²+c
Esta equação descreve esse comportamento de uma forma bem simples, imagine uma esfera, e aplique a equação, essa esfera seria igual a outras duas esferas, e por sua vez essas duas esferas são constituídas de 2 esferas menores, ou seja um paradoxo, e a imagem descrevendo esse processo é mais incrível ainda.

A teoria do caos também possui ligações com o efeito borboleta, na verdade acho que os dois constituem a mesma dinâmica. É uma das coisas mais misteriosas e belas no universo.
Tudo no universo tende ao caos, nossa existência é simplesmente insignificante diante do universo e por conta disso parece que estamos sempre a salvos (Um dos principais fatores é o tempo).
Essa teoria não foi aceita facilmente até hoje, mas podemos ver que ela se encaixa em varias perspectivas.
Do caos a ordem pode surgir por mais breve que ela seja.
-Felipe Aiello
Biografia:
http://www.turingarchive.org/viewer/?id=476&title=2
http://www.rose-hulman.edu/mathjournal/archives/2002/vol3-n1/paper1/v3n1-1pd.pdf
http://ac.els-cdn.com/S0960982295001849/1-s2.0-S0960982295001849-main.pdf?_tid=97b95d0e-855b-11e3-9bac-00000aab0f6b&acdnat=1390611598_34025411ad8a5c4a814149eec0f1f510
http://www.dailymotion.com/video/x14x9cx_a-vida-secreta-do-caos-documentario-2009_tech
0 comentários:
Postar um comentário